segunda-feira, 7 de setembro de 2020

ESTADOS DE ENERGIAS QUÂNTICO DE GRACELI.

se tem sensibilidades térmicas diferentes conforme os tipos de materiais e tipos de energias que são empregadas, provando assim que os estados de energias e quântico variam conforme são empregadas tipos diferenciados de energias.

ou seja, com amesma temperatura se tem sensibilidades variadas conforme esta temperaura foi produzida sobre um esmo material.

e o mesmo acorre sobre materiais diferenciados.

ou seja, estados de energias variados em mesmos materiais, e também em materiais diferenciados.

X

TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI

TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.

FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS =

TRANSFORMAÇÕES ⇔ INTERAÇÕES  ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE  ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔  Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS,  ⇔   Δ MASSA , ⇔ Δ  CAMADAS ORBITAIS ,  ⇔  Δ FENÔMENOS  ,  ⇔  Δ DINÂMICAS, ⇔  Δ VALÊNCIAS, ⇔  Δ BANDAS,  Δ entropia e de entalpia,  E OUTROS.

x

$\left(\alpha _{0}mc^{2}+\sum _{{j=1}}^{3}\alpha _{j}p_{j}\,c\right)\psi ({\mathbf {x}},t)=i\hbar {\frac {\partial \psi }{\partial t}}({\mathbf {x}},t)$ [EQUAÇÃO DE DIRAC].

$\Delta U={\frac {3}{2}}nR(T_{f}-T_{i})$ + FUNÇÃO TÉRMICA.

$N=N_{{o}}.e^{{-\lambda .t}}$ + FUNÇÃO DE RADIOATIVIDADE

$T=e^{-2bL}$ , $b={\sqrt {\frac {8\pi ^{2}m(Ub-E)}{h^{2}}}}$

$\Delta S=S_{2}-S_{1}=\int _{1}^{2}{\frac {\delta Q}{T}}$ + ENTROPIA REVERSÍVEL

+   $\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}$ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA

$E_{p}={\sqrt {{\frac {\hbar c^{5}}{G}}}}\approx$ ENERGIA DE PLANCK

X

$V [R] [MA] = Δ e, M, Δ f, Δ E, Δ t, Δ i, Δ T, Δ C, Δ E, Δ A, Δ D, Δ M......$

ΤDCG

X

Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli +
DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..

DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
x

sistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].

x

número atômico, estrutura eletrônica, níveis de energia

[comprimento de onda (λ).

$\Delta \mathrm {E} =hf=hc/\lambda$

onde c, velocidade da luz, é igual a $f\lambda$ .]

X

TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.

X

CATEGORIAS DE GRACELI

T l   T l    E l      Fl        dfG l

N l   El             tf l

P l   Ml           tfefel

Ta l   Rl

         Ll

D

X

$\left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigg (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigg )},$ [ESTADO QUÂNTICO]

Espaço de fases ou espaço fásico é definido como o espaço formado pelas posições generalizadas e seus momentos conjugados correspondentes. Se emprega no contexto da mecânica lagrangiana e a mecânica hamiltoniana. Usualmente se designa o espaço fásico ou uma parte dele por Γ (gamma maiúscula). Fisicamente cada ponto do espaço fásico representa um possível estado do sistema mecânico.

Em física estatística se usam distribuições de probabilidade definidas sobre o espaço fásico. Partindo de certo subconjunto das distribuições de probabilidade de um espaço fásico pode construir-se uma estrutura de espaço de Hilbert. Estes espaços de Hilbert de um sistema clássico são a base para os espaços de Hilbert que aparecem na mecânica quântica.

Espaço de fases na mecânica clássica[editar | editar código-fonte]

Em mecânica clássica o espaço de fases é uma construção matemática a partir do espaço de configuração. Concretamente um espaço de fases adequado para um sistema com um número finito de graus de libertade é um fibrado tangente do espaço de configuração do sistema mecânico. Esse fibrado tangente construído dessa maneira pode ainda ser dotado de uma topologia simplética onde podem formular-se convenientemente os teoremas da mecânica hamiltoniana.

Um dos teoremas clássicos sobre espaços de fases é o teorema de Liouville, segundo o qual uma nuvem de pontos distribuídos de acordo com uma densidade de probabilidade que represente um estado de equilíbrio macroscópico ρ(p_i,q_i) deve ser invariável no tempo.

Além disto cada hamiltoniano H definido sobre um espaço de fases está associado a um conjunto de trajetórias de evolução temporal. O conjunto de trajetórias constitui uma foliação unidimensional do espaço de fases que recobre quase todo o espaço de fases (concretamente todo o espaço de fases, salvo um conjunto de medida nula), este último equivale a que o espaço pode ser descomposto em trajetórias que não se intersectam.

Espaço de fases em mecânica quântica[editar | editar código-fonte]

Uma das características distintas da mecânica quântica é que o estado físico de um sistema não determina o resultado de qualquer medida que possa fazer-se sobre ele. Em termos mais simples, o resultado de uma medida sobre dois sistemas quânticos que tenham o mesmo estado físico nem sempre resulta nos mesmos resultados. Assim uma teoria como a mecânica quântica que trata de descrever a evolução temporal dos sistemas físicos só pode prever a probabilidade de que ao medir uma determinada grandeza física se obtenha determinado valor. Isto quer dizer que a mecânica quântica realmente é uma teoria que explica como varia a distribuição de probabilidade das possíveis medidas de um sistema (entre duas medições consecutivas, já que no instante da medida se produz um colapso da função de onda aleatório).

O estado quântico de um sistema pelas razões anteriormente expostas não se parece em nada ao estado clássico de uma partícula ou um sistema de partículas. De fato o estado quântico de um sistema é representável mediante uma função de onda:

$\Phi \in L_{\mu }^{2}(\Gamma )$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

A relação mais próxima entre espaço fásico e função de onda é que o quadrado do módulo da função de onda está relacionado com uma distribuição de probabilidade definida sobre o espaço fásico. Isto significa que, para construir o conjunto de estados quânticos ou espaço de Hilbert de certos sistemas quânticos, pode considerar-se inicialmente o espaço fásico que se usaria em sua descrição clássica e considerar o conjunto de funções de quadrado integrável sobre o espaço fásico, a este tipo de procedimento se conhece como quantização.

Na mecânica clássica, a função de Lagrange, lagrangiana ^{(português brasileiro)} ou lagrangiano ^{(português europeu)} ( ${\mathcal {L}}$ ) de um sistema é uma função expressa em termos das coordenadas generalizadas $q_{i}$ , da taxa de variação dessas coordenadas (velocidades generalizadas) ${\dot {q}}_{i}$ e do tempo t, e dada matematicamente pela diferença entre a energia cinética ( $T$ ) e a energia potencial generalizada ( $U$ ) do sistema:

${\mathcal {L}}_{(q_{i},{\dot {q}}_{i},t)}=T-U$
X

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

.^{[Ref. 1]}^{[Ref. 2]}^{[Ref. 3]}

Por padrão a energia potencial é função apenas das coordenadas generalizadas (sistemas conservativos) e/ou do tempo, contudo, a exemplo do que observa-se para o caso eletromagnético, quando na forma adequada, admite-se o uso de um potencial "generalizado", esse função também das velocidades generalizadas. O potencial eletromagnético generalizado^[1]^{[Ref. 3]} permite a descrição de partículas elétricas imersas em campos eletromagnéticos via Mecânica de Lagrange, a exemplo. Forças dissipativas proporcionais às velocidades generalizadas também são admissíveis via potenciais dissipativos, a exemplo o potencial dissipativo de Rayleigh.^[2]^[3] ^{[Ref. 3]}

A lagrangiana é termo central na integral temporal que define o que se denomina em Física por ação. Diferente da Mecânica de Newton, junto com o princípio de Hamilton da ação em extremo, a lagrangiana e a Mecânica de Lagrange definem toda a dinâmica de um sistema sem recorrer a vetores e diagramas vetoriais, fazendo-o de forma a usar essencialmente funções escalares. Nesses termos a lagrangiana porta-se como uma equação fundamental do sistema a qual associa-se, encerrando em si todas as informações acerca do sistema. Pode-se pois, a partir dela e do formalismo atrelado à Mecânica de Lagrange, obter qualquer informação desejada acerca do sistema. A lagrangiana possui dimensões de energia, joules no S.I..^{[Ref. 1]}^{[Ref. 2]}^{[Ref. 3]}

Associado à lagrangiana de um sistema, via Transformada de Legendre, tem-se o hamiltoniano ${\mathcal {H}}$ do sistema, essa uma função das coordenadas generalizadas $q_{i}$ , dos momentos conjugados generalizados $p_{i}$ e do tempo t. O Hamiltoniano $H_{(q_{i},p_{i},t)}$ , definido por H = T + U, também caracteriza uma equação fundamental, e juntamente com o formalismo da Mecânica de Hamilton, constitui formalismo alternativo plenamente equivalente ao de Lagrange no que tange à descrição da dinâmica do sistema.^{[Ref. 2]} Tais formalismos encontram importante aplicação também dentro da relatividade.^{[Ref. 4]}

Embora amplamente aplicada ao campo da dinâmica de energia e matéria, o cálculo variacional não limita o raciocínio à campos específicos da Física. Diversos problemas nas mais variadas áreas mostram-se suscetíveis ao tratamento similar.

Exemplos[editar | editar código-fonte]

Mecânica[editar | editar código-fonte]

Partícula livre

Uma partícula livre move-se em ausência de força resultante, idealmente em ausência de força aplicada. Logo sua lagrangiana define-se apenas por sua energia cinética em caso limite.

${\mathcal {L}}=T-U=T={\frac {1}{2}}m[{\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}]$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

onde, conforme convenção, ${\dot {x}}={\frac {dx}{dt}}=v_{x}$

X

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

e assim por diante.

Para movimento confinado ao plano xy, e em coordenadas polares:

$x=r\cos \theta$

$y=r\sin \theta$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

de onde, derivando-se:

${\dot {x}}={\dot {r}}\cos \theta -r{\dot {\theta }}\sin \theta$

${\dot {y}}={\dot {r}}\sin \theta +r{\dot {\theta }}\cos \theta$

Quadrando-se as velocidades generalizadas e com o auxílio de algumas relações trigonométricas tem-se pois que:

${\mathcal {L}}_{(r,{\dot {r}},\theta ,{\dot {\theta }},t)}={\frac {1}{2}}m[{\dot {r}}^{2}+{(r{\dot {\theta }})}^{2}]$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

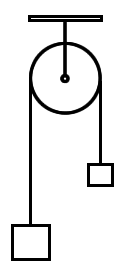
Máquina de Atwood

Máquina de Atwood. No texto, x corresponde à distância da massa da esquerda (massa M1) até a linha horizontal que passa pelo centro do disco. A altura da massa M2 é l-x, onde l representa tamanho total de corda em suspensão.

Na máquina de Atwood, considerando g a aceleração da gravidade, M₁ a massa da esquerda e M₂ a massa da direita, a energia potencial do sistema escreve-se:

$U=-M_{1}gx-M_{2}gy$ ,

X

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

uma vez adotado o nível de referência como sendo uma linha horizontal a passar pelo centro do disco. Nessa situação x e y representam os tamanhos em suspensão da corda que sustentam respectivamente as massas M₁ e M₂.

Há um vínculo entre x e y de tal forma que $x+y=c$ é uma constante, o tamanho total de corda em suspensão. Nesses termos, basta uma coordenada generalizada para descrever-se o problema, à escolha, x, e reescreve-se a energia potencial gravitacional como:

$U=-M_{1}gx-M_{2}g(c-x)$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Em uma máquina de Atwood ideal a polia e a corda têm massas desprezíveis se comparadas às massas M₁ e M₂. Nesse caso a energia cinética total se escreve:

$T={\frac {1}{2}}M_{1}\left({\frac {dx}{dt}}\right)^{2}+{\frac {1}{2}}M_{2}\left({\frac {d(c-x)}{dt}}\right)^{2}={\frac {1}{2}}(M_{1}+M_{2}){\dot {x}}^{2}$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

e a função de Lagrange escreve-se:

$L_{(x,{\dot {x}},t)}=T-U={\frac {1}{2}}(M_{1}+M_{2}){\dot {x}}^{2}+M_{1}gx+M_{2}g(c-x)$
$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

que encerra em si toda informação necessária ao cálculo da dinâmica do sistema.

Seguindo-se com o formalismo de Lagrange, tem-se que a equação de movimento deve satisfazer à equação de Lagrange:

${\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)-{\frac {\partial L}{\partial q_{i}}}=0$ .

X

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Neste caso há apenas uma coordenada generalizada, q_i = x. Determinando-se as derivadas tem-se:

${\frac {\partial L}{\partial x}}=(M_{1}-M_{2})g$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

${\frac {\partial L}{\partial {\dot {x}}}}=(M_{1}+M_{2}){\dot {x}}$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

${\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)=(M_{1}+M_{2}){\ddot {x}}$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Levando os resultados à equação de Lagrange tem-se a equação diferencial para o sistema:

${\ddot {x}}=a={\frac {M_{1}-M_{2}}{M_{1}+M_{2}}}g$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

onde a é a aceleração das massas. Tal equação é análoga à obtida via aplicações diretas da lei de Newton conforme descrito em artigo específico, conforme esperado.

A equação horária para x obtém-se com facilidade doravante mediante integração, sendo a resposta análoga à de um movimento retilíneo uniformemente variado com aceleração constante $a={\ddot {x}}$ :

$x_{(t)}=X_{0}+V_{0}t+{\frac {1}{2}}\left({\frac {M_{1}-M_{2}}{M_{1}+M_{2}}}g\right)t^{2}$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

com $X_{0}$ e $V_{0}$ correspondendo a constantes, respectivamente o comprimento em suspensão inicial da corda para a massa M₁ e a velocidade descendente inicial (no sentido de x crescente) da massa M₁, determinados no instante em que zera-se o tempo (t=0s).

O teorema de Liouville é um resultado da mecânica hamiltoniana sobre a evolução temporal de um sistema mecânico. Considera-se um conjunto de partículas com condições iniciais próximas que podem ser representadas no espaço de fases por uma região conexa, a qual, apesar de se expandir e contrair a medida que cada partícula evolua, manterá invariante seu volume.

Há também resultados matemáticos relacionados em topologia simplética e teoria ergódica.

Consideremos uma região do espaço fásico que evolua com o tempo ao deslocar-se sobre sua trajetória. Cada um de seus pontos transforma-se ao longo do tempo em uma região de localizada forma diferente, a qual se situa em outra parte do espaço fásico. O teorema de Liouville afirma que, apesar da translação e a alteração de forma, o "volume" total desta região permanecerá invariante. Além disso, devido à continuidade da evolução temporal, se a região for conexa inicialmente, seguirá sendo conexa todo o tempo.

Quase todas as demostrações usam o fato de que a evolução temporal de uma "nuvem" de pontos no espaço fásico é de fato uma transformação canônica que alterará a forma e posição de tal nuvem, ainda que mantenha seu volume total.

Demonstração direta[editar | editar código-fonte]

Uma forma de ver provada que a evolução temporal é uma transformação canônica, fato relativamente perceptível, e a partir daí calcular diretamente o determinante de tal alteração de coordenadas, é provar que de fato o determinante de tal transformação é igual a 1, o qual prova a invariância do volume.

Demonstração baseada na forma simplética[editar | editar código-fonte]

Outra forma de provar o teorema é ter em conta que a forma de volume ${\eta }_{\Gamma }\;$ do espaço fásico é o n-ésimo produto da forma simplética, e que está de acordo com o teorema de Darboux, expressando-se como produto de pares de variáveis canonicamente conjugadas:

${\eta }_{\Gamma }=\bigwedge _{i=1}^{n}\omega =\omega \land \dots \land \omega =dp_{1}\land \dots \land dp_{n}\land dq_{1}\land \dots \land dq_{n}=dP_{1}\land \dots \land dP_{n}\land dQ_{1}\land \dots \land dQ_{n}$

X

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

De onde segue que o determinante da transformação é igual a 1 e, portanto:

$\forall V\subset \Gamma :\quad \int _{V}d^{n}\mathbf {q} d^{n}\mathbf {p} =\int _{\phi _{\tau }(V)}d^{n}\mathbf {Q} d^{n}\mathbf {P}$
$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Essa última expressão é essencialmente o enunciado do teorema de Liouville.

Equação de Liouville[editar | editar código-fonte]

O teorema de Liouville pode ser reescrito em termos do colchete de Poisson. Essa forma alternativa, conhecida como equação de Liouville, vem a ser dada por:

${\frac {\partial \rho }{\partial t}}=-\{\,\rho ,H\,\}$
$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

ou em termos do operador de Liouville, também chamado "Liouvilliano":

${\hat {\mathbf {L} }}=\sum _{i=1}^{d}\left[{\frac {\partial H}{\partial p_{i}}}{\frac {\partial }{\partial q^{i}}}-{\frac {\partial H}{\partial q^{i}}}{\frac {\partial }{\partial p_{i}}}\right],$
$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

que leva à forma:

${\frac {\partial \rho }{\partial t}}+{\hat {\mathbf {L} }}\rho =0.$
$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Mecânica quântica[editar | editar código-fonte]

Em mecânica quântica existe um resultado análogo ao teorema de Liouville que descreve a evolução de um estado misto. De fato, pode-se chegar à versão mecânico-quântica deste resultado mediante a simples quantização canônica. Aplicando esse procedimento formal, chegamos ao análogo quântico do teorema de Liouville:

${\frac {\partial }{\partial t}}\rho =-{\frac {i}{\hbar }}[H,\rho ]$
$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Onde ρ é a matriz densidade. Quando se aplica o resultado ao valor esperado de um observável, a correspondente equação dada pelo teorema de Ehrenfest toma a forma:

${\frac {d}{dt}}\langle A\rangle ={\frac {i}{\hbar }}\langle [H,A]\rangle$
$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Onde $A\,$ é um observável.

A física estatística é o ramo da física que usa métodos da teoria das probabilidades e estatística e, particularmente, as ferramentas matemáticas para lidar com grandes populações e aproximações, na solução de problemas físicos. Pode descrever uma grande variedade de campos com uma natureza inerentemente estocástica. Suas aplicações incluem muitos problemas nos campos da física, biologia, química, neurologia e até mesmo em algumas ciências sociais, como a sociologia. Seu principal objetivo é esclarecer as propriedades da matéria sob conjuntos, em termos de leis físicas que regem o movimento atômico.^[1]

Em particular, a mecânica estatística desenvolve os resultados fenomenológicos da termodinâmica a partir de uma análise probabilística dos sistemas de base microscópica. Historicamente, um dos primeiros tópicos da física onde foram aplicados métodos estatísticos foi o campo da mecânica, que se preocupa com o movimento de partículas ou objetos quando submetidos a uma força.

Mecânica estatística[editar | editar código-fonte]

Ver artigo principal: Mecânica estatística

A mecânica estatística fornece um quadro que relaciona as propriedades microscópicas de átomos e moléculas com as propriedades macroscópicas ou extensivas de materiais que podem ser observados na vida cotidiana. Portanto, ela explica a termodinâmica como um resultado natural da estatística, mecânica clássica e mecânica quântica ao nível microscópico. Por causa desta história, a física estatística é muitas vezes considerada como sinônimo de mecânica estatística ou termodinâmica estatística.

Uma das equações mais importantes da mecânica estatística (análogo à F = ma em mecânica, ou a equação de Schrödinger na mecânica quântica) é a definição da função de partição Z, que é essencialmente uma soma ponderada de todos os possíveis estados q disponíveis para um sistema .

$Z=\sum _{q}{\mathrm {e} ^{-{\frac {E(q)}{k_{B}T}}}}$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

$V$

onde $k_{B}$ é a constante de Boltzmann, T é a temperatura e E(q) é a energia do estado q. Além disso, a probabilidade de um determinado estado q ocorrer é dada por

$P(q)={\frac {\mathrm {e} ^{-{\frac {E(q)}{k_{B}T}}}}{Z}}$

$X$

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Aqui, vemos que os estados de energia muito alta têm pouca probabilidade de ocorrência, um resultado que é consistente com a intuição.

A abordagem estatística pode funcionar bem em sistemas clássicos quando o número de graus de liberdade (e assim o número de variáveis) é tão grande que a solução exata não é possível, ou não é realmente útil. A mecânica estatística também pode descrever o trabalho na dinâmica não-linear, teoria do caos, física térmica, dinâmica dos fluidos (particularmente nos números de Knudsen elevados) e física de plasmas.

Embora alguns problemas em física estatística possam ser resolvidos analiticamente por meio de aproximações e expansões, as pesquisas mais atuais utilizam o poder de processamento de computadores modernos para simular ou aproximar soluções. Uma abordagem comum para problemas estatísticos é usar uma simulação de Monte Carlo para produzir uma ideia da dinâmica de um sistema complexo.

Como os plasmas são muito bons condutores, os potenciais elétricos têm um papel importante. O potencial médio que existe no espaço entre partículas carregadas, independentemente da questão de como ele pode ser medido, é chamado de "potencial de plasma" ou "potencial do espaço". Se um eletrodo é inserido em um plasma, o seu potencial em geral ficará consideravelmente abaixo do potencial do plasma, devido à chamada bainha de Debye. A boa condutividade elétrica dos plasmas faz com que os seus campos elétricos sejam muito pequenos. Disso resulta o importante conceito de "quase neutralidade", que diz que a densidade das cargas negativas é aproximadamente igual à das cargas positivas para grandes volumes de plasma (n_e = <Z>n_i), mas na escala do comprimento de Debye pode haver desequilíbrio de cargas. No caso especial em que camadas duplas são formadas, a separação das cargas pode se estender por algumas dezenas de comprimentos de Debye.

A magnitude dos potenciais e campos elétricos pode ser determinada por outros meios do que simplesmente encontrando-se a densidade de carga resultante. Um exemplo comum é assumir que os elétrons satisfazem a relação de Boltzmann:

$n_{e}\propto e^{e\Phi /k_{B}T_{e}}$ .
X
V

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

Diferenciando-se esta relação, obtém-se um meio para calcular o campo elétrico a partir da densidade:

${\vec {E}}=(k_{B}T_{e}/e)(\nabla n_{e}/n_{e})$ .
X

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS

É possível produzir um plasma que não seja quase neutro. Um feixe de elétrons, por exemplo, só tem cargas negativas. A densidade de um plasma não neutro deve geralmente ser muito baixa, pois de outra forma ele será dissipado pela força eletrostática de repulsão.

Em plasmas astrofísicos, a triagem Debye (atenuação do campo elétrico provocada pela presença de portadores de carga móveis) impede que os campos elétricos afetem diretamente o plasma por grandes distâncias, isto é, maiores do que o comprimento de Debye. Mas a existência de partículas carregadas faz com que o plasma gere e seja afetado por campos magnéticos. Isto pode causar (e efetivamente causa) um comportamento extremamente complexo, como a geração de camadas duplas no plasma, um objeto que separa as cargas por algumas dezenas de comprimentos de Debye. A dinâmica de plasmas interagindo com campos magnéticos externos e auto-gerados é estudada na disciplina acadêmica de magnetoidrodinâmica.

Assinar: Postagens (Atom)